Deep Neural Network Nonlinear Model Predictive Control for CSTR

Introduction

The Continuous Stirred Tank Reactor (CSTR) is a fundamental model in chemical engineering, representing a reactor where the contents are well-mixed, ensuring uniform composition and temperature throughout. This report delves into the mathematical modeling of a CSTR, its simulation, and control using a Nonlinear Model Predictive Control (NMPC) strategy integrated with a neural network for predictive behavior.

CSTR Model

The CSTR dynamics are governed by the mass and energy balance equations:

\[\frac{dC}{dt} = \frac{F}{V}(C_{in} - C) - k(T)C\]

\[\frac{dT}{dt} = \frac{F}{V}(T_{in} - T) + \frac{-\Delta H}{\rho C_p}k(T)C + \frac{Q}{\rho C_p V}\]

The reaction rate is:

\[-r_A = k(T)C_A = k_0 e^{\left( \frac{-E}{RT} \right)}C_A\]

Parameter	Value Description
Initial Flow Rate	Initial volumetric flow rate
Initial Temperature	Initial temperature
Initial Concentration	Initial concentration
Reactor Radius	Reactor radius
Reaction Rate Constant	Reaction rate constant
Activation Energy/Gas Const	Activation energy/gas constant
Heat Transfer Coefficient	Overall heat transfer coefficient
Density	Density
Specific Heat Capacity	Specific heat capacity
Heat of Reaction	Heat of reaction
Small Value	Small value
Mass Fractions	Mass fractions
Input Parameters	Input parameters

Parameter Equations

$$ F_0 = 0.1~\mathrm{m}^3/\mathrm{min} $$

$$ T_0 = 350.0~\mathrm{K} $$

$$ c_0 = 1.0~\mathrm{kmol}/\mathrm{m}^3 $$

$$ r = 0.219~\mathrm{m} $$

$$ k_0 = 7.2 \times 10^{10}~\mathrm{min}^{-1} $$

$$ \frac{E_b}{R} = 8750~\mathrm{K} $$

$$ U = 54.94~\mathrm{kJ}/(\mathrm{min}\cdot\mathrm{m}^2\cdot\mathrm{K}) $$

$$ \rho = 1000~\mathrm{kg}/\mathrm{m}^3 $$

$$ C_p = 0.239~\mathrm{kJ}/(\mathrm{kg}\cdot\mathrm{K}) $$

$$ \Delta H = -5 \times 10^4~\mathrm{kJ}/\mathrm{kmol} $$

$$ \varepsilon = 1 \times 10^{-5}~\mathrm{m} $$

$$ x_s = [0.878,,324.5,,0.659] $$

$$ u_s = [300,,0.1] $$

Nonlinear Model Predictive Control (NMPC)

NMPC optimizes control inputs over a prediction horizon to minimize deviations from desired setpoints while respecting constraints.

Parameters

\[N = 15, \quad dt = 0.25\;\text{seconds}, \quad Tf = 3.75\;\text{seconds}\]

Cost Function

\[J = \sum_{k=t}^{t+N-1} L(x_k, u_k) + M(x_{t+N})\]

Where:

\[L(x_k, u_k) = (x_k - x_{\text{ref},k})^\top Q (x_k - x_{\text{ref},k}) + (u_k - u_{\text{ref},k})^\top R (u_k - u_{\text{ref},k})\]

\[M(x_{t+N}) = (x_{t+N} - x_{\text{ref},t+N})^\top P (x_{t+N} - x_{\text{ref},t+N})\]

Weights:

\[Q = \text{diag}(1.0 / \textbf{xs}^2), \quad R = \text{diag}(1.0 / \textbf{us}^2)\]

\[\begin{split}P = \begin{bmatrix} 5.9298 & -8.4e{-4} & -1.5454e{-2} \\ -8.4e{-4} & 7.75e{-6} & 2.31e{-5} \\ -1.5454e{-2} & 2.31e{-5} & 2.5945 \end{bmatrix}\end{split}\]

Constraints

\[\begin{split}\textbf{umin} = \begin{bmatrix} 0.95 \\ 0.85 \end{bmatrix} \times \textbf{us}, \quad \textbf{umax} = \begin{bmatrix} 1.05 \\ 1.15 \end{bmatrix} \times \textbf{us}\end{split}\]

ACADOS Configuration

• Solver: SQP / SQP-RTI

• Integrator: IRK

• QP Solver: PARTIAL_CONDENSING_HPIPM

• Condensing: Full ($N$ intervals)

• Regularization:

\[\lambda_{\text{LM}} = 1e^{-5}\]

Neural Network Integration

Data Preparation

• Gather time-series data: concentration, temperature, inflow, heat input

• Scale input/output:

\[\mathbf{X}_{\text{scaled}} = \frac{\mathbf{X} - \mu_{\mathbf{X}}}{\sigma_{\mathbf{X}}}\]

Neural Network Architecture

• Input: $ \mathbf{a}_0 = \mathbf{x} $

• Hidden layers:

\[\mathbf{a}_i = \text{ReLU}(\mathbf{W}_i \mathbf{a}_{i-1} + \mathbf{b}_i)\]

• Output:

\[\mathbf{y} = \mathbf{W}_{\text{out}} \mathbf{a}_{\text{last}} + \mathbf{b}_{\text{out}}\]

Training

• Loss: Mean Squared Error

\[\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (\hat{\mathbf{Y}}_i - \mathbf{Y}_i)^2\]

• Optimizer: Adam or SGD

\[\mathbf{W}_{\text{new}} = \mathbf{W}_{\text{old}} - \alpha \nabla \text{MSE}\]

• Validation: Prevent overfitting using a held-out validation set.

Results

Training loss over epochs

DNN-NMPC simulation results for CSTR

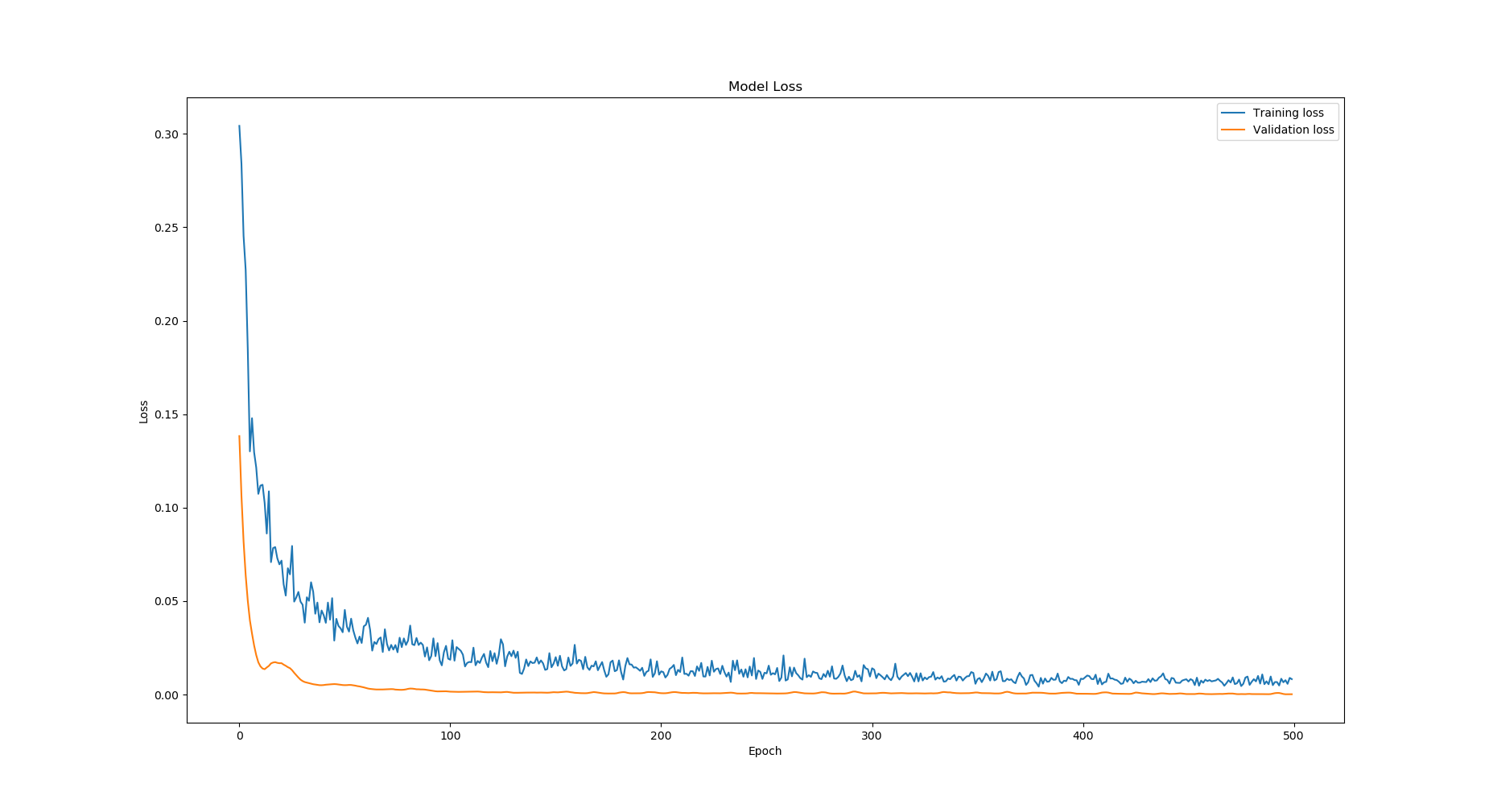
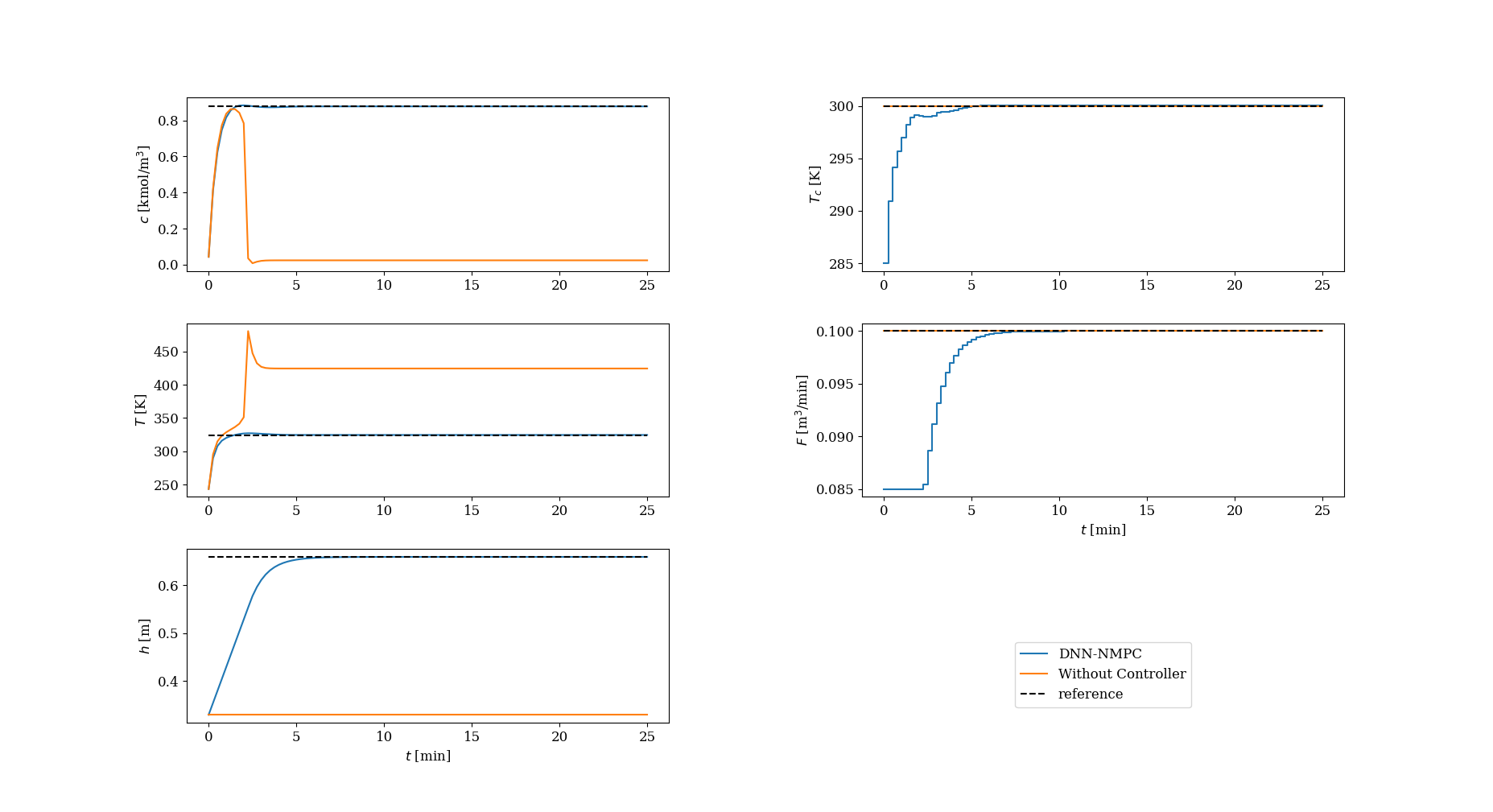
Conclusion

The CSTR model, integrated with a neural network and controlled via NMPC, represents a sophisticated and powerful approach for managing complex chemical systems. This architecture allows for efficient real-time control and adaptation to dynamic operating conditions.